Atwood machine
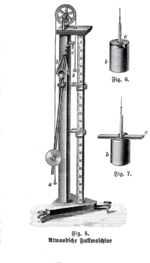
The Atwood machine (or Atwood's machine) was invented in 1784 by the English mathematician George Atwood as a laboratory experiment to verify the mechanical laws of motion with constant acceleration. Atwood's machine is a common classroom demonstration used to illustrate principles of classical mechanics.
The ideal Atwood machine consists of two objects of mass m1 and m2, connected by an inextensible massless string over an ideal massless pulley.[1]
Both masses experience uniform acceleration. When m1 = m2, the machine is in neutral equilibrium regardless of the position of the weights.
Equation for constant acceleration
[edit]
An equation for the acceleration can be derived by analyzing forces. Assuming a massless, inextensible string and an ideal massless pulley, the only forces to consider are: tension force (T), and the weight of the two masses (W1 and W2). To find an acceleration, consider the forces affecting each individual mass. Using Newton's second law (with a sign convention of ) derive a system of equations for the acceleration (a).
As a sign convention, assume that a is positive when downward for and upward for . Weight of and is simply and respectively.
Forces affecting m1: Forces affecting m2: and adding the two previous equations yields and the concluding formula for acceleration
The Atwood machine is sometimes used to illustrate the Lagrangian method of deriving equations of motion.[2]
See also
[edit]- Frictionless plane – simple kinematic model of an object on a ramp under gravity
- Kater's pendulum – Reversible free swinging pendulum
- Spherical cow – Humorous concept in scientific models
- Swinging Atwood's machine – Variation of Atwood's machine incorporating a pendulum
Notes
[edit]- ^ Tipler, Paul A. (1991). Physics For Scientists and Engineers (3rd, extended ed.). New York: Worth Publishers. p. 160. ISBN 0-87901-432-6. Chapter 6, example 6-13
- ^ Goldstein, Herbert (1980). Classical Mechanics (2nd ed.). New Delhi: Addison-Wesley/Narosa Indian Student Edition. pp. 26–27. ISBN 81-85015-53-8. Section 1-6, example 2
External links
[edit]- A treatise on the rectilinear motion and rotation of bodies; with a description of original experiments relative to the subject by George Atwood, 1764. Drawings appear on page 450.
- Professor Greenslade's account on the Atwood Machine
- Atwood's Machine by Enrique Zeleny, The Wolfram Demonstrations Project









